Karl-Heinz Brakhage, Alice C. Niemeyer, Wilhelm Plesken, Daniel Robertz, Ansgar Strzelczyk
Retaining the combinatorial Euclidean structure of a regular icosahedron, namely the 20 equiangular (planar) triangles, the 30 edges of length 1, and the 12 different vertices together with the incidence structure, we investigate variations of the regular icosahedron admitting self-intersections of faces. We determine all rigid equivalence classes of these icosahedra with non-trivial automorphism group and find one curve of flexible icosahedra.
This Documentation contains formal algebraic and numerical data and visualizations of the icosahedra classified in the above paper. The first part is concerned with the rigid icosahedra (Sections 1-4 and Section 6 for the visualization), the second contains a visualization of the curve of icosahedra (Section 5).
Rigid icosahedra
Table 1 lists the relevant information of the icosahedra with non-trivial symmetry in the notation of the paper. In particular each line refers to a formal Gram-matrix out of which \(r_{f,G}\) real-valued Gram-matrices can be obtained resulting in a total of 35 inequivalent icosahedra. The Gram-matrices contain the inner products of the vectors giving the position of the vertices relative to the center of mass. The combinatorial symmetry group of all icosahedra is denoted by \(A \cong C_2\times A_5\). The Euclidean symmetry groups are the subgroups listed in the second column of the table. For the other invariants in Table 1 consult the paper.
Table 1: Summary of formal Gram-matrices with symmetry
| No. | \(S\!:=\!{\rm Stab}_A\) | \( {\rm Syl}_2(S)\) | \( d_G\) | \(r_{1,G} \) | \( r_G \) | \(r_{f,G}\) | \(\mbox{Trace relation}\) |
|---|---|---|---|---|---|---|---|
1 |
\( {C_2}^2\) |
\( \langle a,d\rangle \frac{\bullet -}{+} \) |
\(8\) |
\(4 \) |
\(2\) |
\(\lambda^4-\dots\)\(\lambda^4- \frac{76}{3}\lambda^3+238\lambda^2-\frac{4964}{5} \lambda+\frac{23767}{15}\) |
|
2 |
\( C_2 \times A_5\) |
\(\langle a,b,d\rangle \) |
\(2\) |
\( 2 \) |
\(2\) |
\(\lambda^2-15\lambda+45\) |
|
3 |
\( C_2 \times D_{10}\) |
\(\langle a,d\rangle \frac{-\bullet}{+}\) |
\(2\) |
\( 2 \) |
\(2\) |
\(\lambda^2-15\lambda+\frac{269}{5}\) |
|
4 |
\( {C_2}^2 \) |
\(\langle a,bd\rangle \frac{- +}{+}\) |
\( 2\) |
\( 2 \) |
\( 2\) |
\(\lambda^2-\frac{71}{5}\lambda+\frac{10561}{225}\) |
|
5 |
\( C_2 \times D_{10}\) |
\(\langle a,d\rangle \frac{-+}{+} \) |
\(4\) |
\( 2 \) |
\(2\) |
\(\lambda^4-\dots\)\(\lambda^4-18\lambda^3+\frac{583}{5}\lambda^2-\frac{1658}{5}\lambda +\frac{9101}{25}\) |
|
6 |
\(C_2 \times D_{6}\) |
\(\langle a,d\rangle \frac{-+}{+} \) |
\(4\) |
\( 4 \) |
\(2\) |
\(\lambda^4-\dots\)\(\lambda^4-26\lambda^3+243\lambda^2-970\lambda +1397\) |
|
7 |
\({C_2}^2 \) |
\(\langle a, bd \rangle\frac{-+}{+} \) |
\(24\) |
\( 10 \) |
\(6\) |
\(\lambda^{12}-\dots\)\( \begin{array}{c} {\lambda}^{12}-{\frac { \left( 2 \right) ^{2} \left( 5179 \right) {\lambda}^{11}}{ \left( 3 \right) ^{2} \left( 5 \right) ^{2}}}+ {\frac { \left( 2 \right) \left( 19 \right) \left( 15333259 \right) {\lambda}^{10}}{ \left( 3 \right) ^{5} \left( 5 \right) ^{4} }}-{\frac { \left( 2 \right) ^{3} \left( 147239694317 \right) {\lambda}^{9}}{ \left( 3 \right) ^{9} \left( 5 \right) ^{4}}}\\ + {\frac { \left( 79 \right) \left( 647 \right) \left( 230403233 \right) {\lambda}^{8}}{ \left( 3 \right) ^{10} \left( 5 \right) ^{3 }}}-{\frac { \left( 2 \right) ^{2} \left( 191 \right) \left( 301320605767 \right) {\lambda}^{7}}{ \left( 3 \right) ^{9} \left( 5 \right) ^{4}}} + { \frac { \left( 2 \right) \left( 83 \right) \left( 11508997 \right) \left( 1837361 \right) {\lambda}^{6}}{ \left( 3 \right) ^{11} \left( 5 \right) ^{3}}}\\ -{\frac { \left( 2 \right) ^{2} \left( 7 \right) \left( 34801471425335039 \right) {\lambda}^{5}}{ \left( 3 \right) ^{13} \left( 5 \right) ^{4}}} + {\frac { \left( 2 \right) \left( 1957611941235953 \right) \left( 3331 \right) {\lambda}^{4}}{ \left( 3 \right) ^{14} \left( 5 \right) ^{4}}}-{\frac { \left( 2 \right) ^{2} \left( 1123 \right) \left( 18722229133 \right) \left( 162739 \right) {\lambda}^{3}}{ \left( 3 \right) ^{13} \left( 5 \right) ^{4}}}\\ +{ \frac { \left( 2 \right) ^{2} \left( 31 \right) \left( 1968103637 \right) \left( 355029313 \right) {\lambda}^{2}}{ \left( 3 \right) ^{14} \left( 5 \right) ^{4}}}-{\frac { \left( 2 \right) ^{3} \left( 2304157 \right) \left( 663613633511 \right) \lambda}{ \left( 3 \right) ^{12} \left( 5 \right) ^{4 }}} + {\frac { \left( 71 \right) \left( 897700968785356223 \right) }{ \left( 3 \right) ^{14} \left( 5 \right) ^{4}}} \end{array}\) |
|
8 |
\({C_2}^2\) |
\(\langle a,b \rangle \frac{--}{-}\) |
\(30\) |
\( 18 \) |
\(6\) |
\(\lambda^5-\dots\)\(\lambda^5-\frac{117}{2}\lambda^4+ 1238\lambda^3-\frac{24063}{2}\lambda^2+{\scriptstyle 53884}\lambda-\frac{179449}{2}\) |
|
9 |
\(C_2\) |
\(\langle a \rangle\quad - \) |
\(172\) |
\( 48 \) |
\(20\) |
\(\lambda^{43}-\dots\)\(\lambda^{43}-\frac{73\cdot 7\cdot 11\cdot 461687}{2^2\cdot3^3\cdot5^2\cdot 29\cdot 79} \lambda^{42} + \frac{857\cdot 120087883773229}{2^7\cdot 3^8\cdot 5^4\cdot 29 \cdot 79}\lambda^{41} - \frac{11^4\cdot 71\cdot 113^2\cdot 337\cdot 10091\cdot 2411}{ 2^{10}\cdot 3^8\cdot 5^4\cdot 29 \cdot 79} \lambda^{40} \pm \cdots \) for full polynomial see Tra688 |
|
10 |
\(D_{10}\) |
\(\langle ad\rangle\quad +\) |
\(2\) |
\( 2 \) |
\(2\) |
\({\lambda}^{2}-{\frac {44}{3}}\,\lambda+{\frac {2131}{45}}\) |
|
11 |
\(D_{6}\) |
\(\langle ad\rangle\quad +\) |
\(2\) |
\( 2 \) |
\(2\) |
\( {\lambda}^{2}-{\frac {68}{5}}\,\lambda+{\frac {1111}{25}}\) |
|
12 |
\( C_2\) |
\( \langle ad\rangle \quad +\) |
\(36\) |
\( 12 \) |
\(8\) |
\(\lambda^{18}-\dots\)\( \begin{array}{c}\lambda^{18} - \frac{1106 \lambda^{17}}{3^2} + \frac{42615911 \lambda^{16}}{3^5 5^2} - \frac{608689958402 \lambda^{15}}{3^9 5^3}\\ + \frac{669379573317764 \lambda^{14}}{3^{11} 5^4} - \frac{542104688910473264 \lambda^{13}}{3^{13} 5^5}\\ + \frac{22353916387655476069 \lambda^{12}}{3^{14} 5^5} - \frac{720294670446150004894 \lambda^{11}}{3^{15} 5^5}\\ + \frac{91982180145192665393491 \lambda^{10}}{3^{16} 5^6} - \frac{625662501440617374450796 \lambda^9}{3^{16} 5^6} \\ + \frac{30690195007521487178466703 \lambda^8}{3^{18} 5^6} - \frac{401321624733542423335145578 \lambda^7}{3^{19} 5^6} \\ + \frac{1389246344510645268761603989 \lambda^6}{3^{19} 5^6} - \frac{11307425831916645400804768766 \lambda^5}{3^{20} 5^6}\\ + \frac{211726641053601153656790047533 \lambda^4}{3^{22} 5^6} - \frac{978251027982988070865732297392 \lambda^3}{3^{23} 5^6}\\ + \frac{3152118264830819298724797047479 \lambda^2}{3^{24} 5^6} - \frac{2107901674869677428030295249866 \lambda}{3^{24} 5^6}\\ + \frac{660819829992992866502773719281}{3^{24} 5^6}\end{array}\) |
|
13 |
\( C_2\) |
\(\langle ad \rangle\quad + \) |
\(168\) |
\( 40\) |
\(24\) |
\(\lambda^{42}-\dots\)\(\lambda^{42}-\frac{ 2 \cdot 719 \cdot 1223 }{ 3^{3} \cdot 5 \cdot 43} \lambda^{41} + \frac{7\cdot 30557\cdot 4091741}{3^6\cdot 5^4\cdot 43 } \lambda^{40} \pm \cdots \) for full file see Tradppm672 |
|
14 |
\( D_{10}\) |
\(\langle ad \rangle \quad +\) |
\(4\) |
\( 2\) |
\(2\) |
\(\lambda^2-\frac{26}{3}\lambda+\frac{149}{9}\) |
Table 2: Clickable information for real Gram matrices
The following table contains visualisations of the different rigid icosahedra accessible by clicking on the links in the second or third column. The visualisations can be controlled via a menu. All visualisations can be rotated by the mouse and scaled by the mouse wheel. Because of the perspective of the camera, the circles and faces in the foreground appear bigger than those in the background.
We recommend the visualisation by inner circles of the triangles. In this case, each triangular face is replaced by its inner circle. In particular the inspheres described in Chapter 6 of the paper which contain several inner circles can be easily detected.
The fourth column shows upon clicking numerical values of the non-zero Eigenvalues of the Gram-matrix. In particular one gets a first idea about the size and the shape of the relevant icosahedron.
The fifth column gives explicit data for an embedding of the icosahedron into 3-space such that that the center of gravity is the origin by listing numerical values for a specific choice of coordinates of the twelve vertices. (The order of the vertices is the one used in the paper, cf. Section 2 of the paper.)
The numbering of the vertices as well as the colours of the faces in the visualisations of the following 35 icosahedra can be read off from the following planar development:
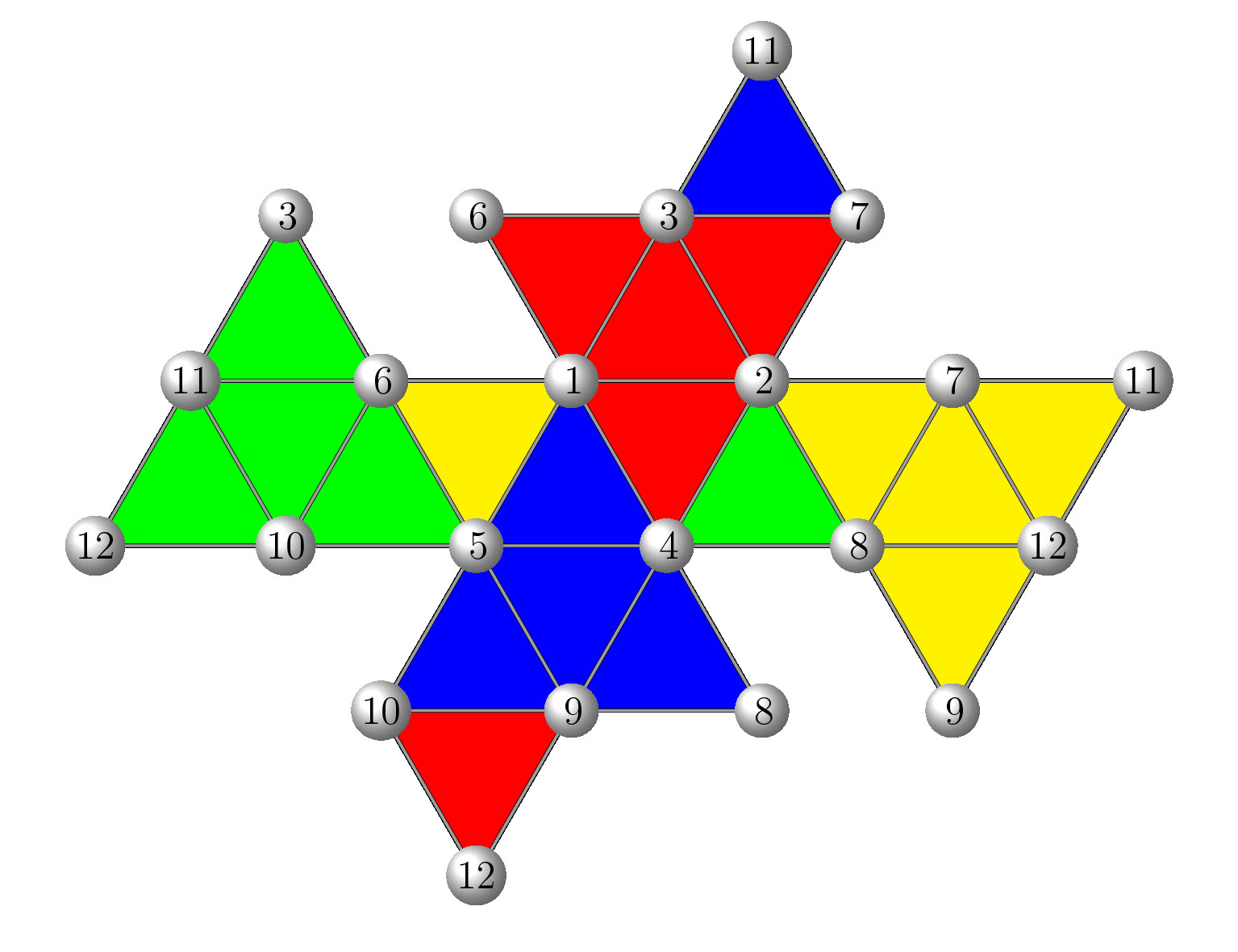
| No. (formal Gram matrix) | Visualisation with inner circles | Visualisation with full faces | nonzero Eigenvalues | Coordinate Matrix |
|---|---|---|---|---|
1 |
1\( (1.65938696466014,\quad 2.14590233070876,\quad 4.00711360248514)\) |
|||
2 |
1\((1.38196601128107, \quad 1.38196601128107,\quad 1.38196601128107)\) 2\(( 3.61803398883097,\quad 3.61803398883097,\quad 3.61803398883097)\) |
|||
3 |
1\( ([1.38196601128107, \quad 1.38196601128107, \quad 3.17082039349175) \) 2\( ([1.82917960677257, \quad 3.61803398883097, \quad 3.61803398883097) \) |
|||
4 |
1\( (1.38196601123635,\quad 1.87639320237135,\quad 1.9782508052213) \) 2\( (2.32360679779885,\quad 3.02174919466013,\quad 3.61803398878951) \) |
|||
5 |
1\( (1.38196601117927,\quad 1.38196601117927,\quad 1.96383495167324) \) 2\( (1.38196601117927,\quad 1.38196601117927,\quad 4.63879617186167) \) |
|||
6 |
1\( (1.50589466677606,\quad 1.50589466677606,\quad 2.2769479397813) \) 2\( (1.66540420066696,\quad 1.66540420066696,\quad 3.48491471391155) \) |
|||
7 |
1\( (1.36377112518488,\quad 1.52763053243019,\quad 2.74199272295777) \) 2\( (1.44208301612537,\quad 1.53336355669567,\quad 1.86660171848005) \) 3\( (1.49469783031344,\quad 2.27147477559889,\quad 2.52911977232753) \) |
|||
8 |
1\( (1.34412281864747, \quad 1.99318601008461, \quad 2.4266307391358) \) |
|||
9 |
1\( (1.46312286960232,\quad 1.66051187698724,\quad 2.66225578140897) \) 2\( (1.49673960075555,\quad 1.79061359666591,\quad 2.56729155940288) \) 3\( (1.66364843883722,\quad 2.11963321956155,\quad 2.30433064476137) \) 4\( (1.44716573098386,\quad 1.46387130221763,\quad 4.55326712162812) \) 5\( (2.03406386383443,\quad 2.52212782613864,\quad 3.71678297456564) \) |
|||
10 |
1\( (1.38196601128916,\quad 1.38196601128916,\quad 2.03519093634195) \) 2\( (2.63147573027191,\quad 3.61803398866916,\quad 3.61803398866916) \) |
|||
11 |
1\( (1.70557280903711,\quad 1.87639320226194,\quad 1.87639320226194) \) 2\( (2.32360679772956,\quad 2.32360679772956,\quad 3.49442719091877) \) |
|||
12 |
1\( (1.31243008016745,\quad 2.02268699666687,\quad 3.53587323898638) \) 2\( (1.96992645848907,\quad 2.18380879188358,\quad 2.52842207878827) \) 3\( (1.50786200975082,\quad 2.36997738061592,\quad 3.53237511847173) \) 4\( (1.4286603994579,\quad 1.86828945304755,\quad 2.5313116458302) \) |
|||
13 |
1\( (1.4730346899396,\quad 2.02809129491186,\quad 2.84614101678436) \) 2\( (1.37192696395679,\quad 1.52665135480779,\quad 2.58098288770463) \) 3\( (1.50469041125417,\quad 1.58321427065314,\quad 3.48813467105417) \) 4\( (1.4718081008245,\quad 1.69221492544181,\quad 2.21171576410269) \) 5\( (1.44653072879576,\quad 1.46410238670219,\quad 4.55350814121647) \) 6\( (1.51331195560146,\quad 1.60336136853891,\quad 2.5758158858235) \) |
|||
14 |
1\( (1.38196601122691,\quad 1.38196601122691,\quad 3.06011329560749) \) |
Curve of flexible icosahedra
Click on the following images to see a curve of flexible icosahedra from various angles:
Click on the following images to see the same curve of flexible icosahedra from the various angles considered above, where the triangular faces are replaced by their inner circles of the triangles.
Acknowledgements
For setting up this internet page we received help from Johannes Flake and Dominik Berhardt. The image of the development was created using the GAP [http://www.gap-system.org] package "SimplicialSurfaces" by Markus Baumeister and Alice Niemeyer. The visualisation for Table 2 were created by Jens Brandt using a Polymake library [(https://polymake.org/doku.php) library three.polymake.js] and the three.js library . The visualisations of the curve of flexible icosahedra were created using Maple "Maple is a trademark of Waterloo Maple Inc.".







